ASME Thickness under external pressure

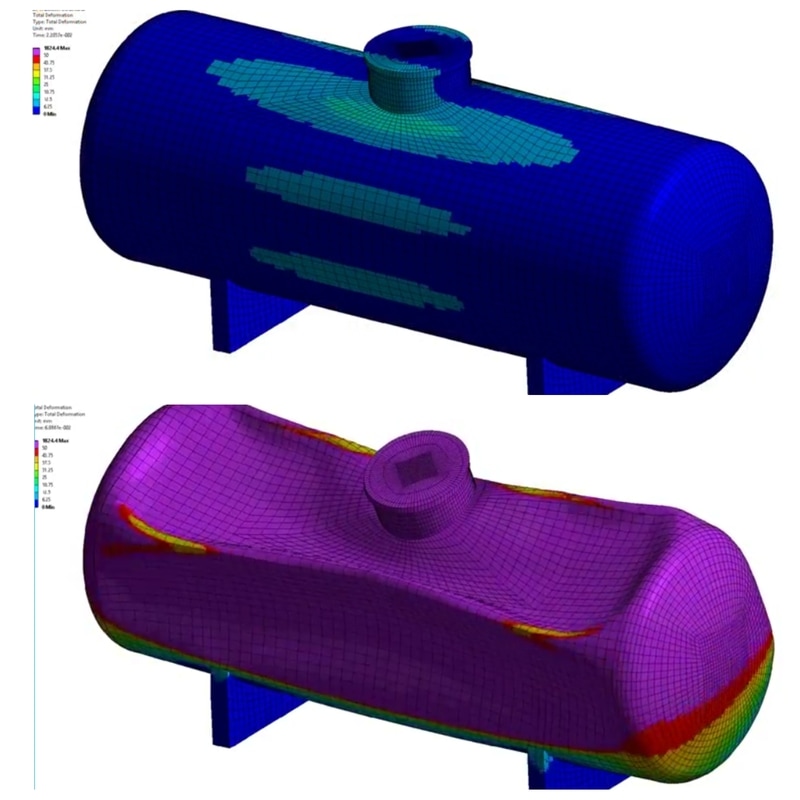
Pressure Vessel with thickness under external pressure.

Question : ในการออกแบบ pressure vessel สักลูก/สักใบ นอกเสียจาก Thickness under internal pressure แล้วนั้น ต้องพิจารณา thickness under external pressure ด้วยหรือไม่ ? ยกตัวอย่าง ในกรณี vessel ทั่วไป ที่ internal pressure > external pressure (เช่น external pressure เป็นความดัน บรรยากาศ) ?
Answer : ต้องพิจารณาครับ

Question : หากเป็นกรณี vessel ทั่วไป เป็นไปได้หรือไม่ ที่ในการออกแบบ ความหนาในส่วนที่รับ external pressure มีค่ามากกว่า ความหนาในส่วนที่รับ internal pressure ?
Answer : มีความเป็นไปได้ ที่การออกแบบ ความหนา(external pressure) > ความหนา(internal pressure), ย้ำอีกทีว่า มี ไม่ใช่ ไม่มี และตกม้าตายกันเยอะ สำหรับ case ที่ออกแบบเฉพาะ ความหนาส่วน internal pressure เพียงอย่างเดียว แล้วนำไปใช้งานจริง

Question : ถ้าอย่างนั้นแล้ว external pressure สามารถเกิดขึ้นได้อย่างไร หรือ มีกรณีไหน ที่เกิดขึ้นได้บ้าง?
Answer : กรณีที่เกิดขึ้นได้ง่ายที่สุด พบเจอบ่อยที่สุด นั่นคือ กรณีที่ ด้านใน vessel เกิด vacuum ในเวลาเดียวกัน กับที่ด้านนอก vessel มีความดันบรรยากาศกระทำ กรณีนี้ชัดเจนที่สุด

                  ยกตัวอย่าง เช่น ในขณะที่มีการ สูบ-ถ่าย/การ flow/การ circulated สารตัวกลางจาก vessel หากอัตราการ flow/circulated ไม่ทัน หรือไม่สัมพันธ์กับการออกแบบ ก็สามารถเกิดกรณีที่ ด้านใน vessel เป็น vacuum ได้ หาก pressure part ไม่สามารถรับแรงที่เกิน plastic หรือ yield deformation ทำให้ความเสียหายจึงบังเกิดขึ้นได้

                  เช่นเดียวกัน กับกรณี vent แรงดัน ภายหลังทำการทดสอบ hydrostatic test หากอัตราการระบายออกไม่ทัน ทำให้มี % ที่ vessel จะเสียหาย จากการยุบตัว/บุบตัวลงไป ของถัง(buckling) เนื่องจาก external pressure มากระทำในขณะที่ด้านใน กำลังวิ่งไปสู่ vacuum และส่วนรับแรงดัน ไม่สามารถทนแรงดันที่กระทำเกิน plastic/yield deformation ได้

                  หรือ อย่างกรณี vessel ที่บรรจุ steam หากมีอัตราการเย็นตัว/ cooling rate ที่เร็วเกินไป สามารถทำให้เกิด vacuum ได้ หากส่วน pressure part ไม่สามารถทนแรงกระทำจาก external pressure ได้ ความเสียหายเกิดขึ้นทันที

Question : แล้วอย่างนี้ ถ้าเราสนใจ จะออกแบบ สำหรับ thickness under internal pressure ตาม ASME เราสามารถ จะไปอ่านที่ไหนบ้าง ?
Answer : Section 8, div 1 และ Section 2, part D-subpart 3 และที่นี่ ที่เดียวที่เป็นภาษาไทย

               ถูกต้องครับพวกเรา Part นี้ ผู้เขียน กำลังจะขยายความ ASME ในส่วนที่เกี่ยวกับเรื่อง external pressure design ใน vessel โดยจะแบ่ง concept เป็น 2 ตอน ตอนแรก(ที่พวกเราอ่านกันอยู่นี้) จะเป็น concept เกี่ยวกับ external pressure load ที่มากระทำกับ vessel โดยมีผลกับการออกแบบ และตอนที่สอง(part หน้า) จะเป็นตัวอย่าง รายการคำนวณ ของงานจริง โดยในส่วนของ thickness under internal pressure หรือ รับแรงดันจากภายใน ผู้เขียนขอข้ามเลยนะครับ เนื่องจากตัวอย่าง หรือ รายละเอียด เนื้อหา พวกเราสามารถตามหา กันได้เยอะแล้ว ทั้งภาษาไทย และ ต่างประเทศ ดังนั้นในหัวข้อนี้ ผู้เขียนจะพูดถึง thickness under external pressure เป็นหลัก เพราะความไม่เข้าใจในหลายๆอย่าง ที่ผู้เขียนพบเจอมา รวมทั้งรายการคำนวณ, หน้างาน, การออกแบบ, การทดสอบ ในหลายต่อหลายครั้ง ที่มักไม่ค่อยกล่าวถึงตรงนี้ ทั้งๆที่ มีความสำคัญ (เป็นลำดับต้นๆในการ design) ดังนั้น พวกเรามาทำความเข้าใจกับมันสักนิดครับ

               ในส่วนที่เกี่ยวข้องกับ Thickness under external pressure ที่พวกเรา คุ้นเคยกับ ASME Section VIII, div.1 part general สำหรับ Cylindrical shell and tube จะอยู่ที่ ug-28 และสำหรับ formed head จะอยู่ในส่วนของ ug-33 โดยที่ thickness under external pressure นั้น จะโยนความสัมพันธ์ในการออกแบบ ส่วนของความหนา pressure part ที่รับแรงดันภายนอก ไปที่ความสำคัญของวัสดุ ที่ใช้ในการออกแบบ(เหมือนเช่นเคย-ASME ค่อนข้างเคี่ยวเรื่องวัสดุ) โดยสรุปคร่าวๆได้ตามนี้

               อ้างอิง: UG-28 (C) กล่าวคือ ถ้าท่านจะออกแบบ ในส่วน pressure part ในส่วนที่รับแรงดันจากภายนอก ตาม ASME section VIII, ท่านต้องมาออกแบบ ตาม code ของวัสดุ ตาม ASME section II, part D. Subpart 3…….ว่างั้น ไม่มีวิธีอื่น นี่จึงเป็นที่มาที่ไป ว่าทำไมเราถึงเลือกเขียนเรื่อง ASME Section II, Part D. Subpart 3 นี้แยกย่อยออกมาเป็นอีกหัวข้อหนึ่ง ใน part นี้เลย

Finite Element Analysis : ความเสียหายที่เกิดขึ้นจาก External pressure

ทุกวันนี้ เรามีโปรแกรม ที่เกี่ยวข้อง กับ Pressure vessel มากมาย ดังนั้น basic หรือ พื้นฐาน พวกเราต้องเข้าใจมันอย่างถ่องแท้ก่อนนะครับ

Concept ที่เกี่ยวข้องกับ external pressure ในการออกแบบ

               พื้นฐาน ทางการออกแบบที่เกี่ยวข้อง ของ external pressure load กล่าวโดยรวม จะมาจาก ทฤษฎีของ failure mechanism ที่กระทำกับ vessel แปลให้เข้าใจง่ายคือ เมื่อมี load ที่เกิดจาก external pressure มากระทำ กับ vessel ของเรา ในที่นี้เราจะเรียกมันว่า P (design pressure) โดยที่ เมื่อใดก็ตามแต่ ที่ความดันภายนอกสูงสุดที่อนุญาตให้กระทำ หรือ MAEWP (Maximum Allowable External Working Pressure) สามารถทนแรง/รับแรง/แรงที่ถูกกระทำ มีค่าน้อยกว่า P (design pressure) เมื่อไหร่ vessel เราบรรลัย (พัง/failure/crush/bulking สุดแล้วแต่เรียก เอาที่สบายใจ) ทันที พื้นฐานทฤษฎีการพัง จะเหมือนกันกับ internal pressure load แต่ต่างกันที่ ตัวแปร

MAEWP > P(design) นั่นคือ ACC

MAEWP < P(design) นั่นคือ REJ

แล้วอะไรบ้าง ที่เป็นปัจจัยที่เกี่ยวข้องกับ MAEWP ?

ug-28 สรุปมาให้พวกเราหมดแล้ว อยู่ที่พวกเรา อ่าน/ไม่อ่าน เท่านั้นเอง

ug-28 สรุป ปัจจัยที่เราต้องพิจารณา ถึง MAEWP หรือ พูดให้ง่ายคือ วิธีคิด MAEWP คิดอย่างไร หาได้อย่างไร ตรงนี้จะมี ตัวแปร ที่พวกเราต้องเจอ อยู่ 2 ตัวหลักๆ คือ ตัวแรก เป็นตัวแปรทางด้านกายภาพ และ ตัวแปรที่สอง ตัวแปรทางด้าน material property ที่ต้องใช้ในการออกแบบ หรือในการหา MAEWP โดยที่ ug-28 จะ link ไปที่ section II, Part D. Subpart 3 ตามที่เรียนแจ้งไว้ข้างต้น ดังนั้น พวกเราเตรียมตัวเปิด สลับกันไป-มา ไป-มา เลยครับ Section VIII-Section II-Section VIII-Section II ตาม concept คร่าวๆ

ASME Section VIII ---> ug-28 ---> condition ---> ASME Section II

ASME Section II ---> Part D. subpart 3 ---> Geometry factor และ Material property

Material property ---> ug-28 ---> calculation ---> MAEWP ---> ACC/REJ

ตัวแปรที่ 1 คือ Factor A

Factor A กล่าวคือ Geometry factor หรือ แฟคเตอร์ที่เกี่ยวกับทางลักษณะทางรูปร่าง ทางกายภาพ ส่วนเว้า ส่วนโค้ง สัดส่วนทางมิติ ต่อความหนา ไม่รู้จะอธิบายเป็นภาษาไทยอย่างไรเหมือนกัน ท่านต้องเข้าใจ ว่ามันคือ factor ทางรูปร่างของ vessel เรา ว่าอย่างนั้น เพราะทาง ASME ก็ไม่ได้มีคำจำกัดความ หรือ มี definition ว่า factor A มันคืออะไรนั่นเอง ตรงนี้มันเป็นความเข้าใจ และดังนั้น เมื่อ Factor A มันคือ แฟคเตอร์ทางกายภาพ สิ่งที่เกี่ยวข้อง หรือ ตัวแปรที่เกี่ยวข้องกับมัน ก็ย่อมที่จะ หลีกเลี่ยงไม่ได้ ที่จะเกี่ยวข้องกับ มิติ ส่วนขนาด(ทั้งส่วนของ ขนาดความยาวส่วนที่พิจารณารับแรง และขนาดเส้นผ่านศูนย์กลาง) และ ส่วนความหนา ที่เป็น ปัจจัยหลัก

รูปที่ 1. Figure G. ใน Subpart 3 section II part D

        เรื่องนี้เป็นเรื่องที่เขียนยาก ผมยอมรับเลย ว่าให้ขึ้นกระดานดำ แล้วเขียนแสดงวิธีทำให้พวกเราดู ง่ายกว่า เขียนอธิบายให้พวกเราอ่านกันบนหน้าจอมือถือ Tablet หรือ หน้าจอคอมพิวเตอร์ แบบนี้ครับ ก่อนอื่นพวกเราเปิดไปที่ Fig. G ของ Subpart 3 of Section II, Part D. จะหน่วย Metric ก็ได้ หรือหน่วย US ก็ได้ พวกเราเปิดเลยครับ ใช้สำหรับ หาค่า FACTOR A (ที่ท่านเห็นในรูป ที่อยู่บน แกน X) เพื่อนำไปคำนวณต่อ

          จาก Geometric chart ที่เราใช้หา factor A พวกเราจะ concentrate หรือ พิจารณาไปที่ ขนาดเส้นผ่านศูนย์กลาง/ความยาวส่วนที่รับแรง/ความหนา ส่วน pressure part ที่เราออกแบบ ทาง ASME จึงสรุปมาเป็น Figure G. ให้พวกเราได้ใช้ ตามรูปที่ 1.ครับ

        กล่าวคือ เราจะหา factor A ได้จากข้อมูลข้างต้น ทีนี้พวกเรา หาค่า FACTOR A ได้แล้วนะครับ

ยากมั้ย? ไม่ยาก…อย่าลืมว่า Factor A ไม่มีหน่วยนะพวกเรา โดยสิ่งที่ต้องพิจารณาคือ L/Do (ที่ท่านเห็นในรูป ที่อยู่บน แกน Y) และ Do/t (ที่ท่านเห็นในรูป อยู่ด้านใน) โดยที่ L/Do อยู่ในช่วง 0.05 ถึง 50 (เขียนอีกรูปแบบหนึ่งคือ 0.05 < L/Do < 50)- L/Do คือ หน่วยของ ความยาว ตัดกับความยาว เช่นเดียวกัน Do/t มันก็คือ หน่วยของ ความยาวตัดกับความยาว หน่วยหายไป ไม่มีหน่วย ลากออกมาเป็น factor A

หาก L/Do มากกว่า 50 ทำไง นายช่าง…ให้พิจารณา ที่ตำแหน่ง L/Do = 50 เลย

หาก L/Do น้อยกว่า 0.05 ทำไง นายช่าง…ก็ให้พิจารณา ที่ตำแหน่ง L/Do = 0.05 เลยครับ

*** โดยที่

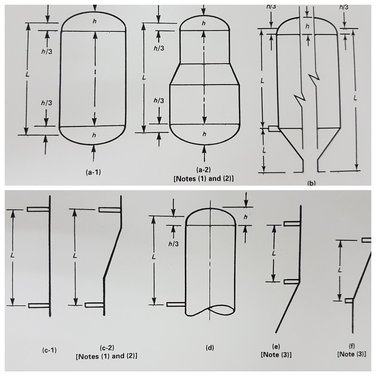
          L    = unsupported length

          Do = outside diameter ถ้าเรารู้ inside diameter เราจะได้ Do = ID + 2t

           t     = vessel thickness คือ ความหนา minimum required thickness คือ ความหนาที่เราต้อง assume หรือ สมมติ ขึ้นมาก่อน เพื่อนำไปคำนวณหาความสามารถในการรับแรงดันจาก external pressure

***จัดว่าเด็ด

          L มันคือ ระยะระหว่าง support ถึง support หรือ ระยะ/ช่วง/ความยาว ระหว่าง stiffening ring ถึง stiffening ring (ไม่ใช่ ระยะความยาวของตัว vessel ทั้งหมด หรือ ความยาว Top to bottom หรือ ความยาวแนวเชื่อม TL-TLนะครับ อย่าสับสน ตรงนี้ในการออกแบบ ค่อนข้างที่จะ make sense และ safety ไปในตัวอยู่แล้ว)

          โดย ใน ASME จะใช้คำว่า

L = design length of a vessel section between lines of support นั่นคือ

L = unsupported length หรือ ส่วนระยะของ ความยาว vessel ในส่วนที่มากที่สุด ที่ไม่มีอะไรรองรับ(เสริมแรง กับตัว vessel)

          ดูรูปเพิ่มเติมที่ FIG ug-28.1 หรือกล่าวคือ พวกเราต้องจินตนาการกันนิดหน่อย ถึง external pressure ที่กำลังกระทำ ต่อ vessel เรา ในช่วงความยาวของ vessel ที่มากที่สุดที่มันสามารถรับได้ คือมันจะไม่พัง ไม่ failure หรือ ไม่เกิดการ bulking ก็สุดตามแต่ ในระยะ L ที่เราออกแบบไว้นั่นเอง

FIG ug-28.1 (รูปบน) ตัวอย่าง Unsupported length (L) กรณีหยาบๆเลย คือ vessel ทั้งลูก ไม่มีส่วน support หรือ รองรับเพื่อกระจายแรงที่กระทำต่อตัว shell เราจะเห็นว่า unsupported length จะมีค่าเท่ากับ ส่วนความยาว shell ทั้งแผง รวมกับ 1/3-ของส่วนหัวถัง

FIG ug-28.1 (รูปล่าง) อธิบาย definition ของคำว่า line of support ได้ค่อนข้างชัดเจน (L) กรณีที่เราออกแบบให้ ส่วนของ shell มี support รองรับ L ก็จะมีค่า เท่ากับ ระยะระหว่าง support นั้นๆ หรือหาก support ไปยังหัวถัง ระยะ L ก็จะมีค่าเท่ากับ ความยาวจาก support + 1/3-ของส่วนหัวถัง

ตัวแปรที่ 2 คือ Factor B

Factor B หาก ผู้เขียนจะให้ definition ของ factor B คร่าวๆ มันคือ material property ที่มีความสามารถในการรับแรงตาม material-temperature chart (วัสดุ-อุณหภูมิ ประมาณนั้น) โดยทั้งนี้และทั้งนั้น พวกเราจะต้องหา ค่าของ factor A มาก่อน จึงจะหาค่าของ factor B ได้ จากการใช้ chart หรือ ใน Subpart 3 of Section II, Part D จะอยู่ในหน้าที่ต่อเนื่องกับ Fig. G นั่นเอง โดยที่ความสัมพันธ์ของ material-temperature factor ที่ท่านต้องเข้าใจ ตาม chart สำหรับ FIG ที่ใช้หา factor B คือ เลือกตามประเภท ของวัสดุ ให้ถูกต้องตาม FIG ยกตัวอย่าง เช่น

FIG

CS x (x คือ 1,2,3,…6)

Material

Carbon steel หรือพวก low alloy steel

ค่าที่พิจารณา

แยกตาม Minimum Yield Strength/ modulus/ design temp

ตัวอย่าง เช่น

516 Gr.70, SA-285 Gr.C ใช้ CS 2

HA x (x คือ 1,2,3,…8)

พวก Stainless steel และพวก Cr Ni alloy

แยกตาม Minimum Yield Strength/ modulus/ design temp

304 ใช้ HA 1
304L ใช้ HA 3
316L ใช้ HA 4 เป็นต้น

NFA x (x คือ 1,2,3,…12)

พวก Aluminum alloy

แยกตาม Minimum Yield Strength/ design temp

Alloy 3003 ใช้ Table NFA 1

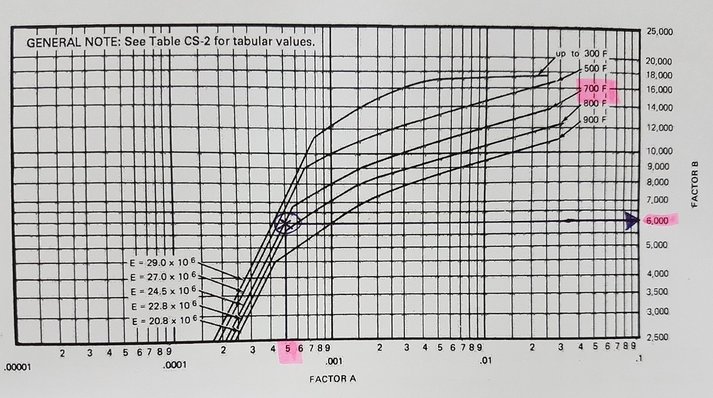
ตัวอย่าง Material-Temperature curve FIG. CS 2 จำพวก min yield 30,000 PSI และแยกตาม modulus of elasticity

ดังนั้น Factor B จะหาได้ จาก factor A ลากไปตัดกับ design temp/ modulus ของ FIG material นั้นๆ(นั่นคือ กรณีปกติ กรณีทั่วไป จุดตัดอยู่บนเส้น บน curve ไม่มีอะไรพิเศษ) หากลาก factor A ไปแล้ว ไม่ตัด กับ design temp/ modulus ของ FIG แล้วนั้น จะแยกเป็น 2 กรณีคือ

กรณี 1 อยู่เลย curve จุดตัดไป เช่น สมมติ หา factor A ได้ 0.05 ที่ design temp 700 Fahrenheit จากภาพด้านบน มันอยู่เลยไป(ไม่ตัดกับเส้นอุณหภูมิ) ให้ลากที่ปลายเส้น 700 Fahrenheit ไปตัด factor B ได้ทันที

กรณี 2 อยู่ก่อนถึง curve เช่นสมมติ หา factor A ได้ 0.0001 ที่ design temp 700 Fahrenheit จากภาพด้านบน มันอยู่ก่อนถึงเส้นอุณหภูมิ หากเกิด กรณี 2 นี้ขึ้น ให้ข้ามไปคำนวณ Pa ตาม ug-28 ได้ทันที

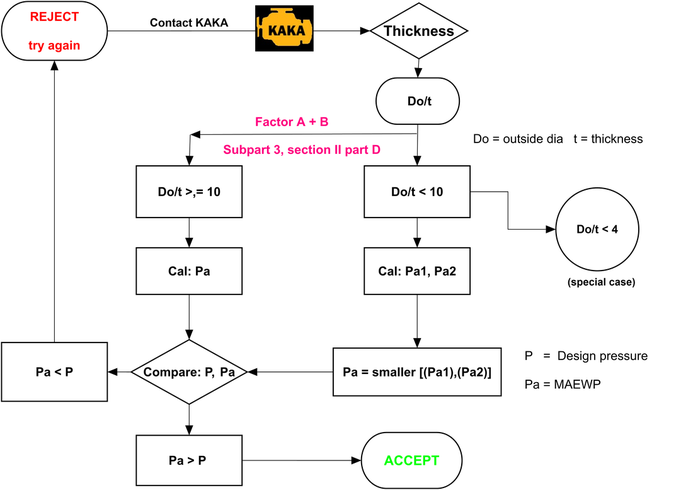
โดยเมื่อเราได้ factor B แล้ว พวกเราจึงสามารถคำนวณต่อไปได้ โดยการใช้ค่าของ factor B ไปคำนวณหา MAEWP (Maximum Allowable External Working Pressure) เพื่อที่จะนำมาเปรียบเทียบกับ Design pressure (ที่เป็น external) ตาม ug-28 ดังที่กล่าวเอาไว้ใน failure mechanism ข้างต้น (พูดให้ง่ายคือ พวกเราจะคำนวณ ความหนาในส่วน pressure part ย้อนกลับ จากความสามารถในการรับแรงดันสูงสุด ที่มันจะไม่พัง) ว่าเงื่อนไขในการออกแบบของเรา ผ่านหรือ ไม่ผ่าน เงื่อนไขการออกแบบ นั่นเองครับ โดย concept ที่เกี่ยวข้อง ตาม flow chart ดังนี้

           บทสรุปจาก Subpart 3, ASME Section II, Part D. ทวนกันอีกครั้ง จาก Factor A และ Factor B ก่อนจะไปวิธีการคำนวณต่อ เราสามารถพิจารณามันออกมาได้ 4 ปัจจัยหลักๆ (1-3 จะเป็น geometry factor, ส่วน 4 จะเป็น material factor) โดยจะวิเคราะห์ความสัมพันธ์ ออกมาเป็นฉากๆ ได้ว่า

          1.Diameter ของ vessel ที่เราออกแบบ หากยิ่ง diameter ใหญ่ ความแข็งแรงในส่วนรับแรงดัน external pressure ยิ่งน้อยลง-ค่อนข้าง make sense เช่นเดียวกับ internal pressure design ครับพวกเรา

          2.ความยาว(ของส่วน unsupported length) หากความยาวเพิ่ม หรือ ส่วนของ unsupported เพิ่ม นั่นจะทำให้ ความแข็งแรงในส่วนรับแรงดัน external pressure ยิ่งน้อยลง (กล่าวคือ ยิ่งยาวมาก ยิ่งเสี่ยงต่อการที่มันจะ bulking ว่างั้น ต่างจาก internal design พี่จะยาวเป็นกิโล ก็ตามสบายครับ) – ถึงเป็นเหตุผล ว่าทำไมมันต้องมี stiffening ring เพื่อที่จะ หลอก stress ว่าระยะ L มันลดลงมานั่นเอง

          3.Thickness หรือ ในส่วนของความหนา ตัวที่บางกว่า ย่อมมี ความแข็งแรงในส่วนรับแรงดัน external pressure น้อยกว่า-ทำนองเดียวกันกับ internal pressure design พวกเราเห็นหรือไม่ครับ

          4.material property ในส่วนของวัสดุที่นำมาออกแบบนั้น ยิ่งเป็นวัสดุที่ yield และ/หรือ modulus of elasticity ต่ำ ก็จะส่งผลให้ ความแข็งแรงในส่วนรับแรงดัน external pressure ต่ำตามลงไป

อ่านถึงตรงนี้ อย่าเพิ่ง งง ครับพวกเรา Part นี้ถ้าอ่านแล้ว งง ไม่ต้องตกใจ เพราะค่อนข้างเข้าใจยากพอสมควร (สาเหตุหลักคือ พวกเรา คุ้นเคยกับ internal pressure มากกว่า) ถ้า part นี้ อ่านแล้ว งง ผู้เขียน แนะนำให้ย้อนครับ ย้อนอ่าน concept อีกครั้ง ตัวแปรหลักๆที่เกี่ยวข้อง มีอะไรบ้าง, ตัวแปรหลักๆที่เกี่ยวข้อง มีความสัมพันธ์ หรือ related ต่อกันอย่างไร เอาเท่านี้ก่อน part นี้ เน้นเข้าใจความสัมพันธ์ สูตรไม่มี ไม่ต้องไปท่อง เครื่องคิดเลขเอาเก็บไปก่อน ไว้ part หน้า ได้ใช้แน่นอน

โดยสำหรับ part หน้า ผู้เขียนจะยกตัวอย่างที่เป็น รายการคำนวณล้วนๆ ที่เกี่ยวข้องกับ external pressure design เห็นภาพ เห็นวิธีการ ชัดเจนแน่นอน โดยเราจะมาดูกันว่า เป็นไปได้หรือไม่ ในการออกแบบ pressure vessel ที่รับ external pressure load เพียงแค่ ความดันบรรยากาศ หรือ 15 psi โดยประมาณ ความหนาในส่วน pressure part จากคำนวณของ external pressure จะมีค่าที่มากกว่า ความหนาที่มาจากการคำนวณ การรับ internal pressure load นั่นเองครับ

ณัฐพงศ์ ไชยสิทธิ์
วุฒิวิศวกรเครื่องกล
วก.958

Vessel ประเภท ที่มีความ(ยาว)สูงมากๆ เช่นจำพวก vessel tower ต่างๆ มี % ที่จะ Buckling จาก external pressure มากกว่า ดังนั้นบ่อยครั้งที่เราจะต้อง ใช้ stiffening ring ช่วยในการออกแบบ เช่น ใบที่เห็นในรูปนี้ครับ